FM and FFM

在CTR预估中，LR模型有着举足轻重的地位，而近几年FM（Factorization Machine）和FFM（Field Factorization Machine）开始在各大比赛和互联网公司广泛运用并取得了不俗的成绩和效果。实际上，FM算是LR的扩展，FFM算是FM的扩展，或者说FMM的一种特例是FM，而FM的一种特例就是LR，下面主要围绕着这两个算法的原理部分展开介绍。

FM

相对于LR模型来说，FM就是考虑了每个特征之间的交互关系，而有些时候在实际场景中这些特征交互往往起到了关键性作用，这也是为什么现在深度学习火的原因之一。打个比方，在广告推荐场景下，一个男性用户可能会有2%的概率点击一条足球属性的广告，而一个年龄在20~40岁之间的男性用户可能会有3%的概率点击，更进一步，满足上面条件的用户在一个给定的上下文条件下，比如世界杯期间、傍晚、甚至在搜索query高度相关的条件下就会有10%的点击概率，这都说明了特征之间的交互作用会对最后的预测结果产生很重要的影响。回到LR模型，它只对每个特征单独赋予一个权重，即

$$\phi(x) = \sigma(w_0 + \sum_i w_i x_i)$$

如果把$\sigma$拿掉的话，只看内部的线性部分，FM模型所能带来的特征交互形式即为

$$\begin{aligned} y(x) =& w_0 + \sum_i w_i x_i +\sum_i \sum_{j = i + 1} w_{ij} x_i x_j\\ = &w_0 + \sum_i w_i x_i +\sum_i \sum_{j = i + 1} <v_i, v_j> x_i x_j \end{aligned}$$

实际上，仅仅依靠$w_{ij}$就可以完成对特征的交互，但这里对$W$矩阵的构造并没有采用直接学习的方式，而是借鉴了矩阵分解的形式，构成形式为由$V \cdot V^T$。这样做的好处有两点，第一点是学习的参数量会显著减少。由于在CTR预估的任务中，会存在非常sparse的特征，百万千万维都有可能，如果直接学习$w_{ij}$的参数量是$N^2$，而如果$V\in R^{N*k}$，学习的参数量就是$kN$，而一般来说$k$的选取并不会太大，一方面是为了减少计算量，另一方面则是为了考虑在高维稀疏特征条件下的泛化性能；第二点是如果直接学习$w_{ij}$，会存在“没什么可学的”的窘境，因为如果是采用SGD的优化方式，$w_{ij}$的更新会依赖那些交互项都不为0的特征，而这样的交互极少，参数可能会学习不充分，但以这种矩阵分解的间接构建$w_{ij}$更新参数就不会出现这种问题。

由于上式前半部分和LR一致，所以我们将重点放在后半部分特征交互项上，经过推导，最后一项可以化简为

$$\begin{aligned} &\sum_i \sum_{j = i+1} <v_i, v_j> x_i x_j \\ =&\frac{1}{2} \sum_i \sum_{j = 1} <v_i, v_j> x_i x_j - 1/2 \sum_i <v_i, v_i> x_i x_i \\ =&\frac{1}{2}(\sum_i \sum_j \sum_{f=1}^{k} v_{i,f} v_{j, f} x_{i} x_{j} - \sum_i \sum_{f=1}^{k} v_{i, f} v_{i, f} x_i x_i) \\ =&\frac{1}{2}\sum_{f = 1}^{k}((\sum_i v_{i,f} x_i)(\sum_j v_{j,f} x_j)) - \sum_i v_{i,f}^2 x_i^2)) \\ =&\frac{1}{2}\sum_{f = 1}^{k}(( \sum_{i=1}^{N} v_{i,f} x_i)^2 - \sum_{i=1}^{N} v_{i,f}^2 x_i^2)) \end{aligned}$$

这里虽然看上去很绕，但只要自己动手写一写就一目了然了。最最重要的是，上面的式子的计算复杂度是线性的$O(kN)$，相比较于直接计算$W$矩阵的复杂度$O(kN^2)$，明显要高效许多。在优化参数时，采用传统的SGD方法，式中各项参数的梯度可求

$$\frac {\partial y(x)}{\partial \theta} = \begin{cases} 1 & \text {if $\theta$ is $w_0$}\\ x_i & \text {if $\theta$ is $w_i$}\\ x_i \sum_j v_{j,f}x_j - v_{i,f}x_i^2 & \text {if $\theta$ is $v_{i,f}$} \end{cases}$$

最后，假设对于一个具体的分类问题，最终带正则的优化目标就变成了

$$\begin{aligned} \theta^* &= argmin_\theta \sum (loss(y(x_i), \hat y_i) + \sum_\theta \lambda \theta^2) \\ &= argmin_\theta \sum -\hat y_i log\sigma(y_i) - (1 - \hat y_i) log(1 - \sigma(y_i)) + \sum_\theta \lambda \theta^2) \end{aligned}$$

FFM

FFM是在FM的基础上引入了Field的概念。从上面的公式中可以看到，FM在处理$x_i$和$x_j$的特征交互时，所使用的隐向量$V$是$v_i$和$v_j$，而在处理$x_i$和$x_k$的特征交互时，所使用的隐向量$V$是$v_i$和$v_k$，这样的局限就是$x_i$和其他所有特征交互时用的都是一个隐向量$v_i$，而FFM对这个问题的处理方法就是引入field的概念，或者说把特征分组，比如年龄特征是一个field，性别特征是一个field，职业特征又是一个field，在FM模型中年龄与性别、职业特征交互项的隐因子$v_{age}$是一样的，但在FFM中性别职业的交互隐因子为$v_{age, sex}$，而性别职业的交互隐因子为$v_{age, prof}$。更一般地，之前的交互项系数的表达为<$v_i, v_j$>，而现在又加入了field这一因素，表达为<$v_{i, f_j}, v_{j, f_i}$>，也就是说在模型的表达式上只需要修改这一项就可以，其余都不变。在实际应用中，我们一般指定分类特征中的每一类特征为一个field，而连续特征每个都为一个field。

我们可以看到，加入field概念之后对特征的交互考虑得更加周全，不同类型的特征交互体现出了多样性，但是由于有这样一个因素的存在，使得我们模型的参数量也随之提高。FM的参数量为$kN$，又由于公式可以化简，因此计算复杂度由初始的$O(kN^2)$变为$O(kN)$，然而FM的参数量则变为了$kfN$，其中$f$为field个数，公式无法化简，计算复杂度为$O(kN^2)$。虽然说由于有field带来的多样性，在$k$的选取上FFM要比FM小，但总体上看FFM的学习速率还是要比FM慢一截。

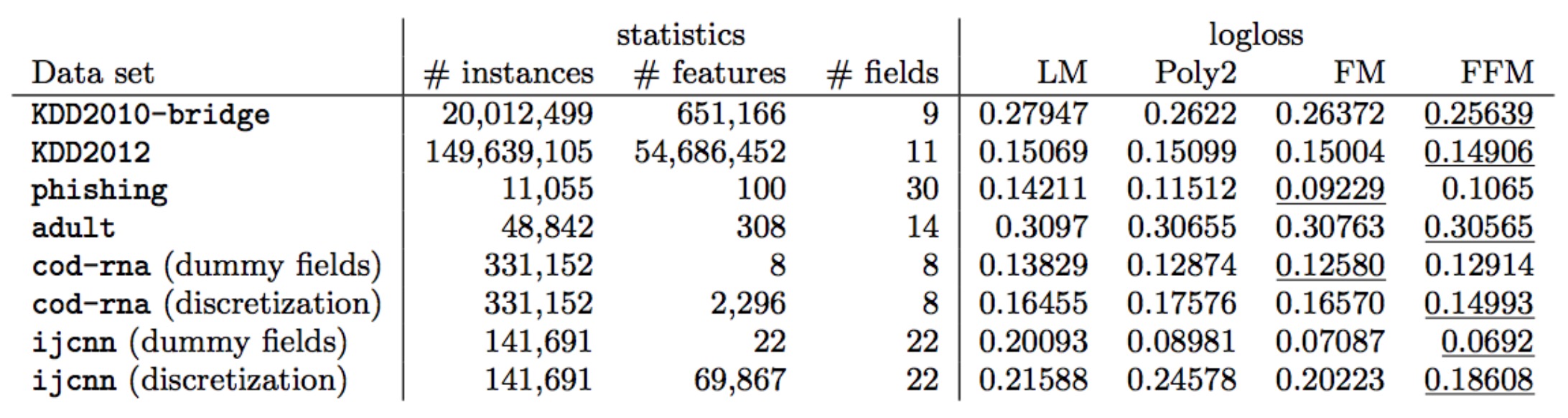
从FM和FFM在公开数据集上的表现来看，FM和FFM各有千秋，但相比于原始未进行特征交互的LM和直接计算特征交互矩阵$W$的Poly2方法还是有一定程度的提升。

参考资料

Factorization Machines
Field-aware Factorization Machines for CTR Prediction